| e-mail: contact@masw.com |
Dispersion Imaging Scheme (Passive-with-Active Scheme)
Passive surface-wave methods for engineering purposes usually deal with surface waves of
cultural origin, especially those caused by traffic (Park and Miller, 2008; Park et al., 2005;
Okada, 2003; Louie, 2001). In case of traffic, surface waves are generated by moving
vehicles as they exert relatively impulsive force onto irregularities on the surface of the road
or trigger transient vibrations on some part of the road structure, such as a bridge, ramp, etc.
For a given survey site, a major part of the recorded surface wave energy usually comes from
those waves generated from only one surface location near the survey site. There may be
other locations contributing relatively weaker energy because they are further away or they
generated weaker energy during a specific recording period. The location of this source
point can be specified by its azimuth (theta) and distance (Ds) from the center of the receiver
spread (Fig. 1).
Existing methods to analyze dispersion of passive surface waves make the assumption of
plane-wave propagation by ignoring the finiteness of the distance between the surveying
area and the origin point of the surface waves. In the spatial autocorrelation (SPAC) method
(Aki, 1957), the issue of azimuth is handled by using a mathematical transformation based
on a symmetric receiver array (e.g., circular) that can cancel out the azimuth factor. The multi-
azimuth case seems to act as a disturbance with this method as well, although some
investigators (for example, Asten, 1983) reported the omni-directional nature can be an
advantage with SPAC. In the wavefield transformation method, on the other hand—for
example, f-k (Capon, 1969) or the imaging method by Park et al. (2004)—this issue is
approached by continuous azimuth scanning with a specific angular increment (e.g., 5
degrees) during the transformation to account for all possibilities of incoming angles. In
particular, Park et al. (2004) tries to sum all the scanned energy for a given single frequency
along the azimuth axis so that energy from multiple azimuths can add up constructively.
Although this approach gives an excellent solution to the issue of azimuth uncertainty,
especially in the case of multi-azimuths, its imaging effectiveness can be significantly
improved in the uni-directional case by accounting for the location of the source point. Once
this source-point location (azimuth and distance) is resolved, then the disper¬sion imaging
process becomes identical to the active method in which relative coordinates of source and
receivers are known. The accurate detection of the azimuth for the source point is far more
important than accurately determining distance (Fig. 2) and this detection algorithm utilizes
the azimuthal scanning method of Park et al. (2004) with significant assistance from the
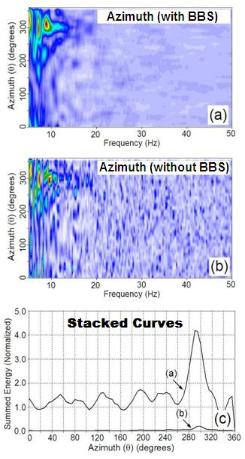
incorporation of the broad-band summation (BBS) technique (Fig. 3).
A field (passive remote) data set recorded by using a 24-channel circular receiver array (Park
et al., 2005) was used to illustrate the effectiveness of using the active scheme after fairly
accurate detection of azimuth (Fig. 4). Fig. 4a is the image obtained by using the normal
passive remote scheme by Park et al. (2004). Then, using the detected azimuth of 290
degrees (Fig. 3), an infinite source distance (i.e., plane-wave propagation) was considered
and the conventional wavenumber (Kx-Ky) concept was applied in the active scheme (Park et
al., 1998a) to result in the image in Fig. 4b. Next, another test was made to estimate the
most probable source distance by progressively increasing the testing distance within 100-
500 m (with an increment of 10 m) on the energy accumulation of the dispersion images.
The estimated distance of 200 m was hen used to complete the source location information
and the active scheme (Park et al., 1998a) was used to give the image in Fig. 4c. All these
images show progressively improved qualities. Furthermore, the broad-band summation
(BBS) technique even further improves the quality when it is incorporated in the active
scheme (Fig. 4d).
Passive surface-wave methods for engineering purposes usually deal with surface waves of
cultural origin, especially those caused by traffic (Park and Miller, 2008; Park et al., 2005;
Okada, 2003; Louie, 2001). In case of traffic, surface waves are generated by moving
vehicles as they exert relatively impulsive force onto irregularities on the surface of the road
or trigger transient vibrations on some part of the road structure, such as a bridge, ramp, etc.
For a given survey site, a major part of the recorded surface wave energy usually comes from
those waves generated from only one surface location near the survey site. There may be
other locations contributing relatively weaker energy because they are further away or they
generated weaker energy during a specific recording period. The location of this source
point can be specified by its azimuth (theta) and distance (Ds) from the center of the receiver
spread (Fig. 1).
Existing methods to analyze dispersion of passive surface waves make the assumption of
plane-wave propagation by ignoring the finiteness of the distance between the surveying
area and the origin point of the surface waves. In the spatial autocorrelation (SPAC) method
(Aki, 1957), the issue of azimuth is handled by using a mathematical transformation based
on a symmetric receiver array (e.g., circular) that can cancel out the azimuth factor. The multi-
azimuth case seems to act as a disturbance with this method as well, although some
investigators (for example, Asten, 1983) reported the omni-directional nature can be an
advantage with SPAC. In the wavefield transformation method, on the other hand—for
example, f-k (Capon, 1969) or the imaging method by Park et al. (2004)—this issue is
approached by continuous azimuth scanning with a specific angular increment (e.g., 5
degrees) during the transformation to account for all possibilities of incoming angles. In
particular, Park et al. (2004) tries to sum all the scanned energy for a given single frequency
along the azimuth axis so that energy from multiple azimuths can add up constructively.
Although this approach gives an excellent solution to the issue of azimuth uncertainty,
especially in the case of multi-azimuths, its imaging effectiveness can be significantly
improved in the uni-directional case by accounting for the location of the source point. Once
this source-point location (azimuth and distance) is resolved, then the disper¬sion imaging
process becomes identical to the active method in which relative coordinates of source and
receivers are known. The accurate detection of the azimuth for the source point is far more
important than accurately determining distance (Fig. 2) and this detection algorithm utilizes
the azimuthal scanning method of Park et al. (2004) with significant assistance from the
incorporation of the broad-band summation (BBS) technique (Fig. 3).
A field (passive remote) data set recorded by using a 24-channel circular receiver array (Park
et al., 2005) was used to illustrate the effectiveness of using the active scheme after fairly
accurate detection of azimuth (Fig. 4). Fig. 4a is the image obtained by using the normal
passive remote scheme by Park et al. (2004). Then, using the detected azimuth of 290
degrees (Fig. 3), an infinite source distance (i.e., plane-wave propagation) was considered
and the conventional wavenumber (Kx-Ky) concept was applied in the active scheme (Park et
al., 1998a) to result in the image in Fig. 4b. Next, another test was made to estimate the
most probable source distance by progressively increasing the testing distance within 100-
500 m (with an increment of 10 m) on the energy accumulation of the dispersion images.
The estimated distance of 200 m was hen used to complete the source location information
and the active scheme (Park et al., 1998a) was used to give the image in Fig. 4c. All these
images show progressively improved qualities. Furthermore, the broad-band summation
(BBS) technique even further improves the quality when it is incorporated in the active
scheme (Fig. 4d).

Fig. 1. Schematic showing spherical and planar propagation of surface waves
generated at relatively close and distance locations, respectively (from Park, 2008).
generated at relatively close and distance locations, respectively (from Park, 2008).
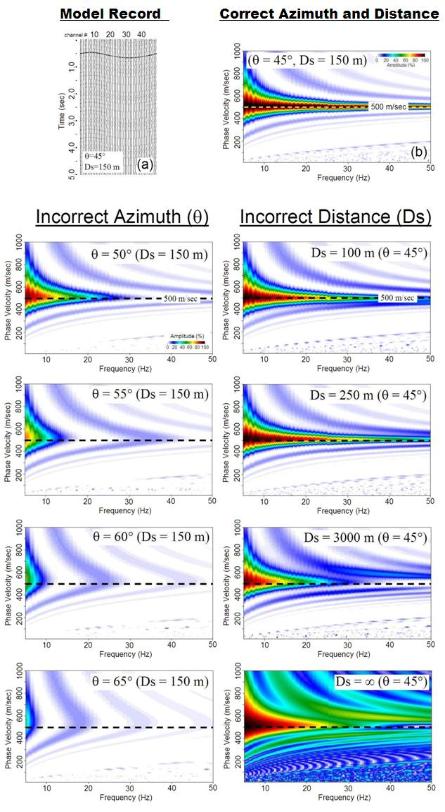
(Right) Fig. 2. Modeling to illustrate the relative
importance of accurate azimuth and distance for a
source point on dispersion imaging (from Park,
2008).
(Left) Fig. 3. Azimuth energy maps from actual
field data set (a) with and (b) without using
broad-band summation (BBS) technique, and (c)
curves obtained from stacking energy along the
frequency axis.
(Below) Fig. 4. Dispersion images obtained from a
field passive remote data set processed by using (a)
the normal passive remote scheme, the active
scheme with (b) detected azimuth and also (c)
detected distance. Broad-band summation (BBS)
technique has been incorporated along with source
location information to generate image in (d).
importance of accurate azimuth and distance for a
source point on dispersion imaging (from Park,
2008).
(Left) Fig. 3. Azimuth energy maps from actual
field data set (a) with and (b) without using
broad-band summation (BBS) technique, and (c)
curves obtained from stacking energy along the
frequency axis.
(Below) Fig. 4. Dispersion images obtained from a
field passive remote data set processed by using (a)
the normal passive remote scheme, the active
scheme with (b) detected azimuth and also (c)
detected distance. Broad-band summation (BBS)
technique has been incorporated along with source
location information to generate image in (d).