Near- and Far-Field Effects of Surface Waves and Dispersion Image
What are "near-field" and "far-field" effects of surface waves?
The influence of both types of effects on the construction of dispersion image is described here.
The optimum offset for a surface-wave survey means a range of distance from the source (often, called offset) where surface waves are best
developed to evaluate the subsurface velocity (Vs) for a planned depth range (e.g., 0-30 m). It is closely related to two field geometry parameters;
source offset (X1) and receiver spread length (L) (see Figure 1). The optimum configuration of these two parameters basically dictates that the offset
should not be too close to and, at the same time, not too far away from the seismic source. The receiver array length (L) determines the longest
wavelength (Wmax) of surface waves that can be measured, which is usually the same as the array length; i.e., Wmax ~ L. Wmax in turn determines
the investigation depth (Zmax) (e.g., Zmax ~ 1/2 Wmax) (Sheriff and Geldart, 1982). Therefore, the receiver array length (L) should be proportional to
investigation depth (Zmax); for example, L ~ 2xZmax. On the other hand, the optimum source offset (X1) sets the minimum distance for surface waves
to be developed. It is important to place receivers beyond this distance because surface waves are not well developed before this distance. Surface
waves are basically formed through interference of P and SV waves. When a vertical seismic source is used, the SV waves can only be effectively
developed through mode-converted refractions and reflections, which will inevitably occur at a certain lateral distance away from the source. This
distance will increase as the SV waves come from deeper part of subsurface rendering the generation of longer-wavelength surface waves more
effective. This means the optimum source offset should change with wavelength; for example, X1 = aW (0.1 <= a <= 1.0) (Park et al., 1999). However,
for a survey that deals with a range of wavelengths to investigate a given depth range (e.g., 0-Zmax), the optimum distance should be set according to
the longest wavelength to be measured (Wmax); i.e., X1 = aWmax ~ aL. This means the source offset (X1) should increase with receiver array length
(L). As a rule of thumb, X1 is usually set to a half of the receiver array length; i.e., X1 = 1/2L.
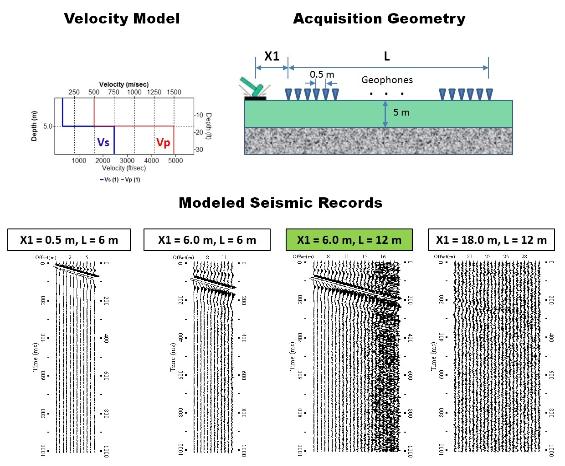
The roles of these two field parameters (X1 and L) are illustrated below based on seismic modeling results. A velocity (Vp and Vs) model is used to
generate synthetic MASW seismic records for different source offsets (X1's) and receiver array lengths (L's) by using the reflectivity method (Fuchs
and Muller, 1971) (Figure 1). Attenuation (Qp and Qs) and density (rho) models are also used for the modeling, which are not displayed here.
Random noise is added during the modeling to more realistically illustrate attenuation of surface waves especially at far offsets. The acquisition
geometry displayed in the figure shows a 0.5-m receiver spacing (dx = 0.5 m) used for all modeling outputs (Figure 1). This means different number of
recording channels are used to make different array lengths; for example, 13 channels to make L = 6.0 m, 25 channels to make L = 12.0 m, and so on.
Modeled seismic records are presented in Figure 1. Dispersion images for modeled seismic records of different X1's and L's are displayed in Figure
2. The common fundamental-mode (M0) theoretical dispersion curve is displayed in each of the dispersion image that is calculated from the velocity
model displayed in Figure 1. Each dispersion image in Figure 2 is explained below in the context of the roles of X1 and L. Similar description for real
field data sets is presented in Figures 3-5 after description of the modeling data sets.
What are "near-field" and "far-field" effects of surface waves?
The influence of both types of effects on the construction of dispersion image is described here.
The optimum offset for a surface-wave survey means a range of distance from the source (often, called offset) where surface waves are best
developed to evaluate the subsurface velocity (Vs) for a planned depth range (e.g., 0-30 m). It is closely related to two field geometry parameters;
source offset (X1) and receiver spread length (L) (see Figure 1). The optimum configuration of these two parameters basically dictates that the offset
should not be too close to and, at the same time, not too far away from the seismic source. The receiver array length (L) determines the longest
wavelength (Wmax) of surface waves that can be measured, which is usually the same as the array length; i.e., Wmax ~ L. Wmax in turn determines
the investigation depth (Zmax) (e.g., Zmax ~ 1/2 Wmax) (Sheriff and Geldart, 1982). Therefore, the receiver array length (L) should be proportional to
investigation depth (Zmax); for example, L ~ 2xZmax. On the other hand, the optimum source offset (X1) sets the minimum distance for surface waves
to be developed. It is important to place receivers beyond this distance because surface waves are not well developed before this distance. Surface
waves are basically formed through interference of P and SV waves. When a vertical seismic source is used, the SV waves can only be effectively
developed through mode-converted refractions and reflections, which will inevitably occur at a certain lateral distance away from the source. This
distance will increase as the SV waves come from deeper part of subsurface rendering the generation of longer-wavelength surface waves more
effective. This means the optimum source offset should change with wavelength; for example, X1 = aW (0.1 <= a <= 1.0) (Park et al., 1999). However,
for a survey that deals with a range of wavelengths to investigate a given depth range (e.g., 0-Zmax), the optimum distance should be set according to
the longest wavelength to be measured (Wmax); i.e., X1 = aWmax ~ aL. This means the source offset (X1) should increase with receiver array length
(L). As a rule of thumb, X1 is usually set to a half of the receiver array length; i.e., X1 = 1/2L.
The roles of these two field parameters (X1 and L) are illustrated below based on seismic modeling results. A velocity (Vp and Vs) model is used to
generate synthetic MASW seismic records for different source offsets (X1's) and receiver array lengths (L's) by using the reflectivity method (Fuchs
and Muller, 1971) (Figure 1). Attenuation (Qp and Qs) and density (rho) models are also used for the modeling, which are not displayed here.
Random noise is added during the modeling to more realistically illustrate attenuation of surface waves especially at far offsets. The acquisition
geometry displayed in the figure shows a 0.5-m receiver spacing (dx = 0.5 m) used for all modeling outputs (Figure 1). This means different number of
recording channels are used to make different array lengths; for example, 13 channels to make L = 6.0 m, 25 channels to make L = 12.0 m, and so on.
Modeled seismic records are presented in Figure 1. Dispersion images for modeled seismic records of different X1's and L's are displayed in Figure
2. The common fundamental-mode (M0) theoretical dispersion curve is displayed in each of the dispersion image that is calculated from the velocity
model displayed in Figure 1. Each dispersion image in Figure 2 is explained below in the context of the roles of X1 and L. Similar description for real
field data sets is presented in Figures 3-5 after description of the modeling data sets.
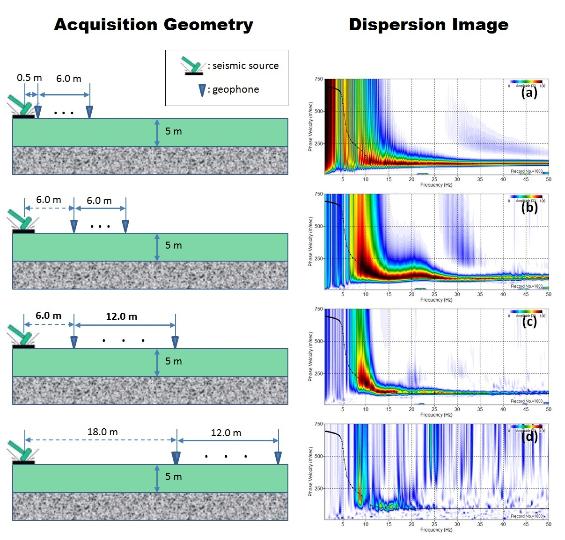
Dispersion Image of Figure 2a (X1 = 0.5 m, L = 6.0 m)
The high-frequency dispersion trend (e.g., ≥ 15 Hz) is well
developed with a sufficient accuracy when compared to the
theoretical M0 curve. This part of the image adequately
represents surface wave velocity of overburden (~100
m/sec). Trends at lower frequencies (e.g., < 15 Hz),
however, lack resolution and tend to deviate from the M0
curve, indicating the resolution of the inversion process for
deeper part of the subsurface (e.g., bedrock) will
deteriorate. This is caused by, first, too small source offset
(i.e., X1 = 0.5 m) for a given receiver array length (i.e., L =
6 m) that prevented recording of surface waves formed
from deeper part of subsurface. Second, the receiver array
length (L) was not long enough to measure such long
wavelengths that penetrate deeper depths. For example, to
measure wavelengths reaching the bedrock at 5-m depth, a
wavelength longer than 10 m has to be measured. This
would require a receiver array of, at least, 10-m length.
Dispersion Image Figure 2b (X1 = 6.0 m, L = 6.0 m)
Because of the increased source offset (X1 = 6 m) in
comparison to the previous case (X1 = 0.5 m), dispersion
trends at low frequencies (e.g., 9-15 Hz) now get more
accurately imaged indicating surface waves penetrating
deeper depths are recorded. However, the influence of
higher modes is apparent at high frequencies (e.g., 20 - 25
Hz) due to the lack of resolution caused by the relatively
short receiver array (L = 6 m) to accurately distinguish
different modes. Resolution of dispersion image increases
with the receiver array length (Park et al., 2001).
Dispersion Image Figure 2c (X1 = 6.0 m, L = 12.0 m)
Now, the receiver array length (L) is sufficiently increased
(L = 12 m) with an accordingly optimal source offset (X1 = 6
m). This configuration makes the dispersion trends achieve
the highest resolution at both low (e.g., ≤ 15 Hz) and high (e.
g., ≥ 20 Hz) frequencies. This acquisition geometry (X1 =
6.0 m and L = 12 m) is considered the most optimum
configuration for the given subsurface model among all four
different configurations tested in Figure 2.
Dispersion Image of Figure 2d (X1 = 18.0 m, L = 12.0 m)
Although the receiver array length is optimally set (L = 12
m), the source offset is excessively long (X1 = 18 m) and all
the receivers are located at the furthest distance from the
source. In consequence, surface waves suffer from severe
attenuation and fall below noise level for most frequency
components by the time they reach the array. Only those
low-frequency surface waves (e.g., ≤ 20 Hz) that underwent
lesser attenuation are vaguely resolved in dispersion
trends. This severe attenuation of surface waves due to
the far-distance of a receiver array is often referred to as
the far-field effect of surface waves.
Figure 2. (right) Acquisition geometries (left column) for different
combination of source offset (X1) and receiver array length (L) and
dispersion images (right column) for corresponding synthetic
seismic records displayed in Figure 1. The common fundamental-
mode (M0) theoretical dispersion is superposed on all dispersion
images that is calculated from the (velocity and density) model
explained in Figure 1.
The high-frequency dispersion trend (e.g., ≥ 15 Hz) is well
developed with a sufficient accuracy when compared to the
theoretical M0 curve. This part of the image adequately
represents surface wave velocity of overburden (~100
m/sec). Trends at lower frequencies (e.g., < 15 Hz),
however, lack resolution and tend to deviate from the M0
curve, indicating the resolution of the inversion process for
deeper part of the subsurface (e.g., bedrock) will
deteriorate. This is caused by, first, too small source offset
(i.e., X1 = 0.5 m) for a given receiver array length (i.e., L =
6 m) that prevented recording of surface waves formed
from deeper part of subsurface. Second, the receiver array
length (L) was not long enough to measure such long
wavelengths that penetrate deeper depths. For example, to
measure wavelengths reaching the bedrock at 5-m depth, a
wavelength longer than 10 m has to be measured. This
would require a receiver array of, at least, 10-m length.
Dispersion Image Figure 2b (X1 = 6.0 m, L = 6.0 m)
Because of the increased source offset (X1 = 6 m) in
comparison to the previous case (X1 = 0.5 m), dispersion
trends at low frequencies (e.g., 9-15 Hz) now get more
accurately imaged indicating surface waves penetrating
deeper depths are recorded. However, the influence of
higher modes is apparent at high frequencies (e.g., 20 - 25
Hz) due to the lack of resolution caused by the relatively
short receiver array (L = 6 m) to accurately distinguish
different modes. Resolution of dispersion image increases
with the receiver array length (Park et al., 2001).
Dispersion Image Figure 2c (X1 = 6.0 m, L = 12.0 m)
Now, the receiver array length (L) is sufficiently increased
(L = 12 m) with an accordingly optimal source offset (X1 = 6
m). This configuration makes the dispersion trends achieve
the highest resolution at both low (e.g., ≤ 15 Hz) and high (e.
g., ≥ 20 Hz) frequencies. This acquisition geometry (X1 =
6.0 m and L = 12 m) is considered the most optimum
configuration for the given subsurface model among all four
different configurations tested in Figure 2.
Dispersion Image of Figure 2d (X1 = 18.0 m, L = 12.0 m)
Although the receiver array length is optimally set (L = 12
m), the source offset is excessively long (X1 = 18 m) and all
the receivers are located at the furthest distance from the
source. In consequence, surface waves suffer from severe
attenuation and fall below noise level for most frequency
components by the time they reach the array. Only those
low-frequency surface waves (e.g., ≤ 20 Hz) that underwent
lesser attenuation are vaguely resolved in dispersion
trends. This severe attenuation of surface waves due to
the far-distance of a receiver array is often referred to as
the far-field effect of surface waves.
Figure 2. (right) Acquisition geometries (left column) for different
combination of source offset (X1) and receiver array length (L) and
dispersion images (right column) for corresponding synthetic
seismic records displayed in Figure 1. The common fundamental-
mode (M0) theoretical dispersion is superposed on all dispersion
images that is calculated from the (velocity and density) model
explained in Figure 1.
Figure 1. (above) Synthetic MASW records of different source offsets (X1's) and receiver array
lengths (L's) are generated (displayed at the bottom) based on the velocity (Vs and Vp) model
shown on top by using the reflectivity method (Fuch and Muller, 1971). Density and attenuation
(Qs and Qp) models are also used during the modeling, but not displayed here. A schematic of
acquisition geometry used for the modeling is displayed on top.
lengths (L's) are generated (displayed at the bottom) based on the velocity (Vs and Vp) model
shown on top by using the reflectivity method (Fuch and Muller, 1971). Density and attenuation
(Qs and Qp) models are also used during the modeling, but not displayed here. A schematic of
acquisition geometry used for the modeling is displayed on top.
After the production survey, a series of field test was
conducted at the center of the survey line by using different
source offsets (X1's) and receiver array lengths (L's). Figure
4a shows surface coordinates of source and receivers for
105) obtained by using the longest receiver array (48-
channel) and the accordingly optimum source offset (X1=
24dx) represents a reference record free of both near- and
far-field effects to be tested hereafter for other test records.
The corresponding dispersion image and extracted
dispersion curve are shown in Figure 4b. This dispersion
curve is used as a reference curve to evaluate the integrity of
dispersion image created from other test records.
Dispersion Image of Figure 4c (X1 = 2dx, L = 5dx)
Because the shortest receiver array (6-CH; L = 10 m) was
used, the dispersion is imaged clearly only for high
frequencies (e.g., ≥ 10 Hz). The source offset (X1 = 2dx) is
slightly under optimal for the given array length.
Dispersion Image of Figure 4d (X1 = 6dx, L = 5dx)
In comparison to the previous case, a slight increase of
source offset resulted in a significant gain of surface wave
energy at lower frequencies (e.g., 7-10 Hz). However, the
resolution of the image at these frequencies is low and the
overall pattern appears to deviate from the reference curve.
This low resolution is caused mainly by the receiver array
length (6-CH; L = 10 m) not long enough.
Dispersion Image of Figure 4e (X1 = 6dx, L = 11dx)
In comparison to the previous case, the extended array
length (12-CH; L = 22 m) now has increased the resolution of
the image, especially at the low frequencies (e.g., 6-10 Hz).
However, when compared to the reference curve, the image
pattern near these low frequencies still appears to have a
minor ambiguity.
Dispersion Image of Figure 4f (X1 = 12dx, L = 23dx)
Now, this further extended receiver array with an accordingly
optimal source offset (X1 = 12dx) has resulted in the image
that most closely follow the reference curve. This means the
configuration (X1 = 12dx and 24-CH array) is most optimal for
this site.
The last dispersion image displayed in Figure 5 shows the far-
field effect of this site. It is noticeable both low and high
frequencies of surface waves attenuated severely due to an
excessively long distance of receiver array from the source
(X1 = 24dx).
Figure 4. (right) (a) The source/receiver (SR) configuration of the five
test field records collected with different source offsets (X1's) and
receiver array lengths (L's) at the center of the production survey
line. Corresponding dispersion images are displayed in (b) - (f).
Figure 5. (below) Dispersion image of a test field record acquired
with an excessively long source offset (X1 = 24dx) at the center of
the production survey line. This illustrates the far-field effect of
surface waves.
conducted at the center of the survey line by using different
source offsets (X1's) and receiver array lengths (L's). Figure
4a shows surface coordinates of source and receivers for
105) obtained by using the longest receiver array (48-
channel) and the accordingly optimum source offset (X1=
24dx) represents a reference record free of both near- and
far-field effects to be tested hereafter for other test records.
The corresponding dispersion image and extracted
dispersion curve are shown in Figure 4b. This dispersion
curve is used as a reference curve to evaluate the integrity of
dispersion image created from other test records.
Dispersion Image of Figure 4c (X1 = 2dx, L = 5dx)
Because the shortest receiver array (6-CH; L = 10 m) was
used, the dispersion is imaged clearly only for high
frequencies (e.g., ≥ 10 Hz). The source offset (X1 = 2dx) is
slightly under optimal for the given array length.
Dispersion Image of Figure 4d (X1 = 6dx, L = 5dx)
In comparison to the previous case, a slight increase of
source offset resulted in a significant gain of surface wave
energy at lower frequencies (e.g., 7-10 Hz). However, the
resolution of the image at these frequencies is low and the
overall pattern appears to deviate from the reference curve.
This low resolution is caused mainly by the receiver array
length (6-CH; L = 10 m) not long enough.
Dispersion Image of Figure 4e (X1 = 6dx, L = 11dx)
In comparison to the previous case, the extended array
length (12-CH; L = 22 m) now has increased the resolution of
the image, especially at the low frequencies (e.g., 6-10 Hz).
However, when compared to the reference curve, the image
pattern near these low frequencies still appears to have a
minor ambiguity.
Dispersion Image of Figure 4f (X1 = 12dx, L = 23dx)
Now, this further extended receiver array with an accordingly
optimal source offset (X1 = 12dx) has resulted in the image
that most closely follow the reference curve. This means the
configuration (X1 = 12dx and 24-CH array) is most optimal for
this site.
The last dispersion image displayed in Figure 5 shows the far-
field effect of this site. It is noticeable both low and high
frequencies of surface waves attenuated severely due to an
excessively long distance of receiver array from the source
(X1 = 24dx).
Figure 4. (right) (a) The source/receiver (SR) configuration of the five
test field records collected with different source offsets (X1's) and
receiver array lengths (L's) at the center of the production survey
line. Corresponding dispersion images are displayed in (b) - (f).
Figure 5. (below) Dispersion image of a test field record acquired
with an excessively long source offset (X1 = 24dx) at the center of
the production survey line. This illustrates the far-field effect of
surface waves.

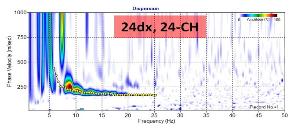
Figure 3. (above) The source/receiver (SR) configuration (top) of all sixteen (16) field records
collected during a production survey conducted by using a 24-channel land streamer. The final 2D
velocity (Vs) cross section obtained by analyzing this data set is displayed at the bottom.
collected during a production survey conducted by using a 24-channel land streamer. The final 2D
velocity (Vs) cross section obtained by analyzing this data set is displayed at the bottom.
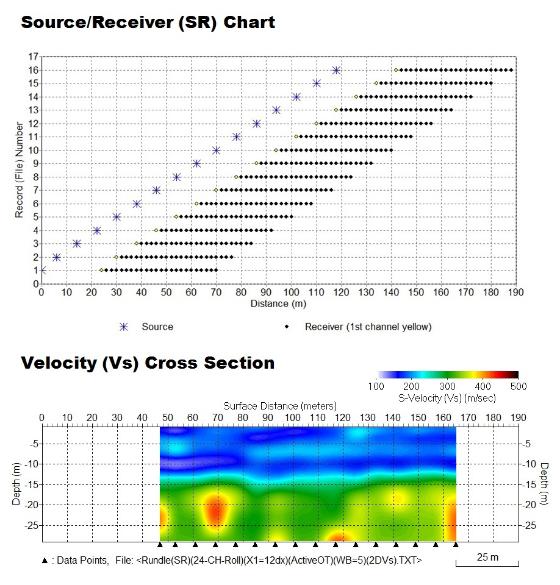
Real Data Example of Near- and Far-Field Effects on Dispersion Image
The effects are illustrated by using actual field data sets acquired during a production MASW survey to generate a 2D velocity cross section. Purpose
of the survey was to characterize stiffness of ground materials for top 25-m depth range. A 24-channel land streamer of 2-m spacing (dx = 2 m) with
4.5-Hz vertical geophones was used. A heavy sledge hammer (16 lb) was used to make impacts at 12dx (24 m) in front of the channel #1. This
source/receiver (SR) configuration moved toward the last channel (#24) direction each time by 4dx (8 m) to collect a total of sixteen (16) field records.
The acquisition geometry for all these records is presented in the SR chart displayed in Figure 3. The final velocity (Vs) cross section analyzed from
this data set is also displayed in the figure. It shows relatively soft materials (soft top soil as confirmed by drilling) (Vs ~ 150 m/sec) of about 15-m
thickness overlying stiff materials (dense silty soil) (250 m/sec ≤ Vs ≤ 400 m/sec) within the investigated depth range of 25 m. Inclusion of the stiffer
layer (Vs ~ 250 m/sec) at approximate depths of 5-10 m is also noticeable in the section, which drilling confirmed as inter-bedded clay layers. In
general, however, there is little variation of subsurface velocities along the lateral direction, rendering the site a layered-earth model.
The effects are illustrated by using actual field data sets acquired during a production MASW survey to generate a 2D velocity cross section. Purpose
of the survey was to characterize stiffness of ground materials for top 25-m depth range. A 24-channel land streamer of 2-m spacing (dx = 2 m) with
4.5-Hz vertical geophones was used. A heavy sledge hammer (16 lb) was used to make impacts at 12dx (24 m) in front of the channel #1. This
source/receiver (SR) configuration moved toward the last channel (#24) direction each time by 4dx (8 m) to collect a total of sixteen (16) field records.
The acquisition geometry for all these records is presented in the SR chart displayed in Figure 3. The final velocity (Vs) cross section analyzed from
this data set is also displayed in the figure. It shows relatively soft materials (soft top soil as confirmed by drilling) (Vs ~ 150 m/sec) of about 15-m
thickness overlying stiff materials (dense silty soil) (250 m/sec ≤ Vs ≤ 400 m/sec) within the investigated depth range of 25 m. Inclusion of the stiffer
layer (Vs ~ 250 m/sec) at approximate depths of 5-10 m is also noticeable in the section, which drilling confirmed as inter-bedded clay layers. In
general, however, there is little variation of subsurface velocities along the lateral direction, rendering the site a layered-earth model.
| e-mail: contact@masw.com |